Summary | Source | Compilation | Precompiled | Execution | Gallery | References
SGFilter
A stand-alone CWEB [1] implementation of the Savitzky—Golay smoothing filter [2], suitable for batch processing of large data streams. For an extensive description of the algorithms used in the program, supported command-line options and syntax, as well as the full documentation of the source, see sgfilter.pdf. [696 kB, 41 pages].
The Savitzky—Golay smoothing filter
The Savitzky—Golay smoothing filter was originally presented in 1964 by Abraham Savitzky [3] and Marcel J. E. Golay [4] in their paper Smoothing and Differentiation of Data by Simplified Least Squares Procedures, Anal. Chem., 36, 1627-1639 (1964) [2]. (Publicly available at http://dx.doi.org/10.1021/ac60214a047.) Being chemists and physicists, at the time of publishing associated with the Perkin-Elmer Corporation (still today a reputable manufacturer of equipment for spectroscopy), they found themselves often encountering noisy spectra where simple noise-reduction techniques, such as running averages, simply were not good enough for extracting well-determined characteristica of spectral peaks. In particular, any running averaging tend to flatten and widening peaks in a spectrum, and as the peak width is an important parameter when determining relaxation times in molecular systems, such noise-reduction techniques are clearly non-desirable.
The main idea presented by Savitzky and Golay was a work-around avoiding the problems encountered with running averages, while still maintaining the smoothing of data and preserving features of the distribution such as relative maxima, minima and width. To quote the original paper [2] on the target and purpose:
»This paper is concerned with computational methods for the removal of the random noise from such information, and with the simple evaluation of the first few derivatives of the information with respect to the graph abscissa. […] The objective here is to present specific methods for handling current problems in the processing of such tables of analytical data. The methods apply as well to the desk calculator, or to simple paper and pencil operations for small amounts of data, as they do to the digital computer for large amounts of data, since their major utility is to simplify and speed up the processing of data.»
The work-around presented by Savitzky and Golay for avoiding distortion of peaks or features in their spectral data is essentially based on the idea to perform a linear regression of some polynomial individually for each sample, followed by the evaluation of that polynomial exactly at the very position of the sample. While this may seem a plausible idea, the actual task of performing a separate regression for each point easily becomes a very time-consuming task unless we make a few observations about this problem. However (and this is the key point in the method), for the regression of a polynomial of a finite power, say of an order below 10, the coefficients involved in the actual regression may be computed once and for all in an early stage, followed by performing a convolution of the discretely sampled input data with the coefficient vector. As the coefficient vector is significantly shorter than the data vector, this convolution is fast and straightforward to implement.
For a derivation of the coefficients used in the Savitzky—Golay convolution kernel, see the documentation sgfilter.pdf [696 kB, 41 pages] extracted from the master CWEB source.
In 2000, editors James Riordon, Elizabeth Zubritsky, and Alan Newman of Analytical Chemistry published a review article [5] summarizing what they had identified as the top-ten seminal papers in the history of the journal, based on the number of citations. Among the listed papers, of which some were written by Nobel-laureates-to-be, the original paper by Savitzky and Golay makes a somewhat odd appearance, as it not only concerns mainly numerical analysis, but also because it actually includes Fortran code for the implementation. The review article [5] concludes the discussion of the Savitzky—Golay smoothing filter with a reminiscence by Abraham Savitzky about the work:
»In thinking about why the technique has been so widely used, I've come to the following conclusions. First, it solves a common problem - the reduction of random noise by the well-recognized least-squares technique. Second, the method was spelled out in detail in the paper, including tables and a sample computer subroutine. Third, the mathematical basis for the technique, although explicitly and rigorously stated in the article, was separated from a completely nonmathematical explanation and justification. Finally, the technique itself is simple and easy to use, and it works.»
As a final remark on the Savitzky—Golay filtering algorithm, a few points on the actual implementation of the convolution need to be made. While the SGFilter program relies on the method for computation of the Savitzky—Golay coefficients as presented in Numerical Recipes in C, 2nd Edn. (Cambridge University Press, New York, 1994), it must be emphasized that the suggestion there presented for the convolution, which is to apply the convlv routine of Numerical Recipes in C, is significantly increasing the complexity and memory consumption in the filtering. In particular, the convlv routine in turn relies on consistent calls to the twofft routine, which in order to deliver proper data needs to be supplied with a return vector of twice the size of the input vector. In addition, convlv requires the size of the input vector to be of an integer power of two (say, M = 1024, 4096, etc.), which may be acceptable for one-off tests but is a rather inconvenient limitation for any more general applications.
Whether the SGFilter program should employ the convolution engine supplied by the convlv routine (recommended by Numerical Recipes in C) or the direct convolution as implemented in the sgfilter routine (recommended by me) is controlled by the CONVOLVE_WITH_NR_CONVLV definition in the sgfilter.h header file. With reference to the above issues with convlv, I strongly advise keeping the default (0) setting for CONVOLVE_WITH_NR_CONVLV.
Current revision
Revision 1.6, as of Wednesday 15 February 2023. Copyright © Fredrik Jonsson 2006-2011, under GPL
Source files
sgfilter.pdf [696 kB] Documentation of the SGFilter program in Portable Document Format (PDF) [6], generated from the PostScript [7] documentation.
sgfilter.w [80 kB]
The CWEB [1] master source code for the SGFilter program.
From this master, the ANSI-C (ISO C99) source code for the program and TeX
code for the documentation is extracted using the CTANGLE and CWEAVE
compilers, respectively.
[ download |
view source ]
sgfilter.tar.gz
[1.99 MB]
Gzip:ed
tape archive of
the entire SGFilter program directory, including the CWEB
[1] master source code source, Makefile:s and all
examples needed to rebuild the program and documentation from scratch.
Requires
CTANGLE and
CWEAVE.
[ download ]
Makefile
[12 kB]
The Makefile for compilation of the executable file, as well as generation
of the documentation of the program. Extracts the C and TeX code from the
CWEB source, and compiles the C and TeX code into binary executable and
PostScript, respectively.
To compile the executable and documentation, simply run 'make' in the
directory containing the source files and this Makefile.
[ download |
view source ]
sgfilter.c
[16 kB]
ANSI-C (ISO C99 conforming source code, extracted from the CWEB master
source code using the
CTANGLE
program by Donald E. Knuth.
[ download |
view source ]
sgfilter.h
[1 kB]
ANSI-C (ISO C99 conforming header, also extracted from the CWEB master
source code.
[ download |
view source ]
sgfilter.tex
[102 kB]
Plain TeX [4] source code, extracted from the CWEB master
source code using the
CWEAVE
program by Donald E. Knuth.
[ download |
view source ]
sgfilter.ps [1.96 MB] PostScript [7] documentation of the SGFilter program, generated from the TeX-code, which in turn is generated from the CWEB master source code.
Compilation
The program is written in CWEB [1], generating ANSI C (ISO C99) conforming source code and documentation as plain TeX-source, and is to be compiled using the sequences as outlined in the enclosed Makefile, which essentially executes two major calls. First, the CTANGLE program parses the CWEB source file sgfilter.w, to extract a C source file sgfilter.c which may be compiled into an executable program using any ANSI C conformant compiler. The output source file sgfilter.c includes #line specifications so that any debugging conveniently can be done in terms of line numbers in the original CWEB source file sgfilter.w. Second, the CWEAVE program parses the same CWEB source file to extract a plain TeX file sgfilter.tex which may be compiled into a PostScript [7] or PDF [6] document. The document file sgfilter.tex takes appropriate care of typographic details like page layout and text formatting, and supplies extensive cross-indexing information which is gathered automatically. In addition to extracting the documentary text, CWEAVE also includes the source code in cross-referenced blocks corresponding to the descriptors as entered in the CWEB source code.
Having executed make (or gmake for the GNU enthusiast) in the same directory where the files sgfilter.w, and Makefile, are located, one is left with the executable file sgfilter, being the ready-to-use compiled program, and the PostScript [7] file sgfilter.ps (or PDF [6] file sgfilter.pdf) which contains the full documentation of the program. Notice that on platforms running any operating system by Microsoft, the executable file will instead automatically be named sgfilter.exe. This convention also applies to programs compiled under the UNIX-like environment CYGWIN.
Precompiled executables
sgfilter [27 kB] Executable program compiled for Mac OS X 10.7 (Lion) using the GNU C Compiler (GCC). [Compiled Saturday 17 Dec, 2011]
Running the program
The SGFilter program is entirely controlled by the command line options supplied when invoking the program. The syntax for executing the program is
sgfilter [options]
where options include the following, given in their long (--) as well as their short (-) forms:
--inputfile ⟨input filename⟩, -i ⟨input filename⟩
Specifies the raw, unfiltered input data to be crunched. The input file should describe the input as two columns containing x- and y-coordinates of the samples, as in the generated input file example-2.0.dat from the example gallery below.
--outputfile ⟨output filename⟩, -o ⟨output filename⟩
Specifies the output file to which the program should write the filtered profile, again in a two-column format containing x- and y-coordinates of the filtered samples. If this option is omitted, the generated filtered data will instead be written to the console (terminal).
-nl ⟨nL⟩
Specifies the number of samples nL to use to the »left» of the basis sample in the regression window (kernel). The total number of samples in the window will be nL + nR + 1.
-nr ⟨nR⟩
Specifies the number of samples nR to use to the »right» of the basis sample in the regression window (kernel). The total number of samples in the window will be nL + nR + 1.
-m ⟨m⟩
Specifies the order m of the polynomial p(x) = a0 + a1(x-xk) + a2(x-xk)2 + ... + am(x-xk) m to use in the regression analysis leading to the Savitzky—Golay coefficients. Typical values are even numbers in the interval between m = 2 and m = 6. Beware of too high values, which easily makes the regression too sensitive, with an oscillatory result.
-ld ⟨lD⟩
Specifies the order of the derivative to extract from the Savitzky—Golay smoothing algorithm. For regular Savitzky—Golay smoothing of the input data as such, use lD = 0. For the Savitzky—Golay smoothing and extraction of derivatives, set lD to the order of the desired derivative and make sure that you correctly interpret the scaling parameters as described in Numerical Recipes in C, 2nd Edn. (Cambridge University Press, New York, 1994).
--help, -h
Display a brief help message and exit clean.
--verbose, -v
Toggle verbose mode. Default: Off. This option should always be omitted whenever no output file has been specified (that is to say, omit any --verbose or -v option whenever --outputfile or -o has been omitted), as the verbose logging otherwise will contaminate the filtered data stream written to the console (terminal).
Example gallery
It is always a good idea to create a rather »nasty» test case for an algorithm, and in this case it also provides the reader of this code with a (hopefully) clear example of usage of the SGFilter program.
We start off with generating a test suite of noisy data, in this case modeling an underlying function g(x) with superimposed Gaussian noise as
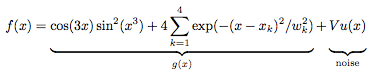
where u(x) is a normally distributed stochastic variable of mean zero and unit variance, V is the local variance as specified arbitrarily, and the remaining parameters (xk,wk) are the positions and widths of four Gaussian peaks superimposed onto the otherwise trigonometric expression for the underlying function. For the current test suite we use (x1,w1) = (0.2,0.007), (x2,w2) = (0.4,0.01), (x3,w3) = (0.6,0.02), and (x4,w4) = (0.8,0.04). These Gaussian peaks serve as to provide various degrees of rapidly varying data, to check the performance in finding maxima. Meanwhile, the less rapidly varying domains which are dominated by the trigonometric expression serves as a test for the capability of the filter to handle rather moderate variations of low amplitude.
The underlying »clean» test function g(x) is shown in Fig. 1. (See the *.eps blocks in the enclosed Makefile for details on how MetaPost [9] was used in the generation of the encapsulated PostScript images shown in Figs. 1-6.)
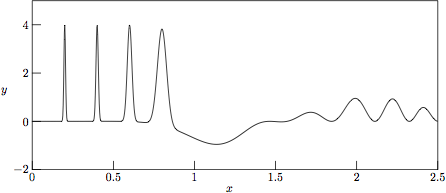
Figure 1.
The underlying »clean» test function
g(x) = cos(3x)
sin2(x3)
+ 4 Σ exp(-(x-xk)2
/ w2k) without any added noise.
Here the positions and widths of the Gaussian peaks are
(x1,w1) = (0.2,0.007),
(x2,w2) = (0.4,0.01),
(x3,w3) = (0.6,0.02), and
(x4,w4) = (0.8,0.04).
[ MetaPost code
(302 bytes) |
Encapsulated PostScript
(122 kB) |
PDF
(26 kB) ]
The generator of artificial test data to be tested by the Savitsky-Golay filtering algorithm is here included as a plain C program, which automatically is generated from the master CWEB [1] source when passed through CTANGLE.
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>
#define TWOPI (2.0*3.141592653589793)
float gauss(float x, float w, float xa) {
return(exp(-pow(((x-xa)/w),2)));
}
float func(float x) {
float retval=gauss(x,0.007,0.2); /* $x_1=0.2$, $w_1=0.007$ */
retval+=gauss(x,0.01,0.4); /* $x_2=0.4$, $w_2=0.01$ */
retval+=gauss(x,0.02,0.6); /* $x_3=0.6$, $w_3=0.02$ */
retval+=gauss(x,0.04,0.8); /* $x_4=0.8$, $w_4=0.04$ */
retval*=4.0;
retval+=cos(3.0*x)*pow(sin(pow(x,3)),2);
return(retval);
}
int main(int argc, char *argv[]) {
int k, mm=1024;
float var=1.0,xmax=2.5, x1, x2, u, v, f, z;
if (argc>1) sscanf(argv[1],"%f",&var); /* Read first argument as variance */
srand((unsigned)time(NULL)); /* Initialize random number generator */
for (k=0;k<mm-1;k+=2) {
x1=xmax*k/((double)mm-1);
x2=xmax*(k+1)/((double)mm-1);
u=((float)rand())/RAND_MAX; /* Uniformly distributed over $[0,1]$ */
v=((float)rand())/RAND_MAX; /* Uniformly distributed over $[0,1]$ */
if (u>0.0) { /* Apply the Box--Muller algorithm on |u| and |v| */
f=sqrt(-2*log(u));
z=TWOPI*v;
u=f*cos(z); /* Normally distributed with E(|u|)=0 and Var(|u|)=1 */
v=f*sin(z); /* Normally distributed with E(|u|)=0 and Var(|u|)=1 */
fprintf(stdout,"%1.8f %1.8f\n",x1,func(x1)+var*u); /* $f(x_1)$ */
fprintf(stdout,"%1.8f %1.8f\n",x2,func(x2)+var*v); /* $f(x_2)$ */
}
}
return(0);
}
After having compiled the above code example.c, simply execute
./example ⟨noise variance⟩ > ⟨file name⟩
in order to generate the test function with a superimposed normally distributed (gaussian) noise of desired variance. In particular, we will in this test suite consider variances of 0 (that is to say, the underlying function without any noise), 0.5, 1.0, and 2.0. Such data files are simply generated by executing [8]
./example 0.0 > example-0.0.dat
./example 0.5 > example-0.5.dat
./example 1.0 > example-1.0.dat
./example 2.0 > example-2.0.dat
The resulting »noisified» suite of test data are in Figs. 2—4 shown for the respective noise variances of V = 0.5, V = 1.0, and V = 2.0, respectively.
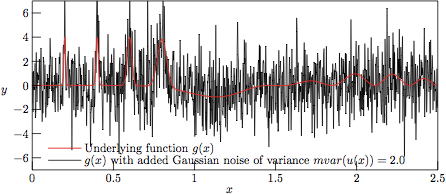
Figure 2.
The test function g(x) with added Gaussian noise of variance
V = 2.0, as stored in file
example-2.0.dat
in the test suite.
[ MetaPost code
(653 bytes) |
Encapsulated PostScript
(200 kB) |
PDF
(51 kB) ]
Applying the Savitzky—Golay filter to the test data is now a straightforward task. Say that we wish to test filtering with polynomial degree m = 4 and ld = 0 (which is the default value of ld, for regular smoothing with a delivered »zero:th order derivative», that is to say the smoothed non-differentiated function), for the two cases nl = nr = 10 (in total 21 points in the regression kernel) and nl = nr = 60 (in total 121 points in the regression kernel). Using the previously generated test suite of noisy data, the filtering is then easily accomplished by executing:
./sgfilter -m 4 -nl 60 -nr 60 -i example-0.0.dat -o example-0.0-f-60.dat
./sgfilter -m 4 -nl 10 -nr 10 -i example-0.0.dat -o example-0.0-f-10.dat
./sgfilter -m 4 -nl 60 -nr 60 -i example-0.5.dat -o example-0.5-f-60.dat
./sgfilter -m 4 -nl 10 -nr 10 -i example-0.5.dat -o example-0.5-f-10.dat
./sgfilter -m 4 -nl 60 -nr 60 -i example-1.0.dat -o example-1.0-f-60.dat
./sgfilter -m 4 -nl 10 -nr 10 -i example-1.0.dat -o example-1.0-f-10.dat
./sgfilter -m 4 -nl 60 -nr 60 -i example-2.0.dat -o example-2.0-f-60.dat
./sgfilter -m 4 -nl 10 -nr 10 -i example-2.0.dat -o example-2.0-f-10.dat
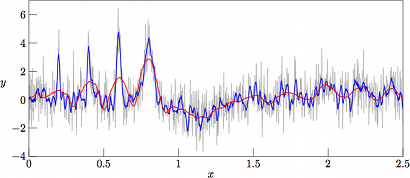
The resulting filtered data sets are shown in Figs. 3—6 for noise variances of V = 2.0, V = 1.0, V = 0.5, and V = 0.0, respectively. The final case corresponds to the interesting case of filtering the underlying function g(x) without any added noise whatsoever, which corresponds to performing a local regression of the regression polynomial to the analytical trigonometric and exponential functions being terms of g(x), a regression where we by no means should expect a perfect match.
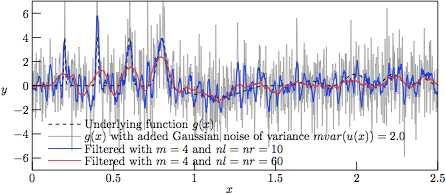
Figure 3.
The profiles resulting from Savitzky—Golay-filtering of the
test function g(x) with added Gaussian noise of variance
V = 2.0.
[ MetaPost code
(1017 bytes) |
Encapsulated PostScript
(343 kB) |
PDF
(92 kB) ]
As can be seen in Fig. 3, the results from filtering the »worst-case» set (with noise variance V = 2.0) with nl = nr = 10 (nl + nr + 1= 21 samples in the regression kernel) and m = 4 (curve in blue) yield a rather good tracking of the narrow Gaussian peaks, meanwhile performing rather poor in the low-amplitude and rather slowly varying »trigonometric hills» in the right-hand side of the graph. As a reference, the underlying function g(x) is mapped in dashed black. On the other hand, with nl = nr = 60 (nl + nr + 1= 121 samples in the regression kernel) and keeping the same degree of the regression polynomial (curve in red), the narrow peaks are barely followed, meanwhile having a rather poor performance in the slowly varying hills as well (albeit of a very poor signal-to-noise ratio).
However, with a lower variance of the superimposed noise, we at V = 1 have a nice tracking of the slowly varying hills by the 121-sample regression kernel, as shown in Fig. 4, meanwhile having a good tracking of the narrow Gaussian peaks by the 21-sample regression kernel. That the 21-sample window is noisier than the 121-sample one should not really be surprising, as the higher number of samples in the regression window tend to smoothen out the regression even further.
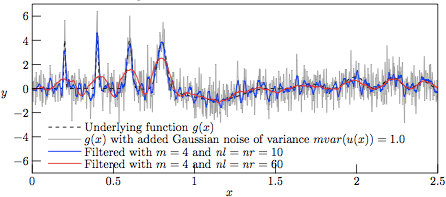
Figure 4.
The profiles resulting from Savitzky—Golay-filtering of the
test function g(x) with added Gaussian noise of variance
V = 1.0.
[ MetaPost code
(1017 bytes) |
Encapsulated PostScript
(343 kB) |
PDF
(91 kB) ]
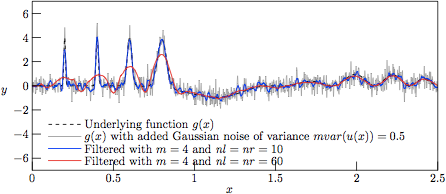
Figure 5.
The profiles resulting from Savitzky—Golay-filtering of the
test function g(x) with added Gaussian noise of variance
V = 0.5.
[ MetaPost code
(1017 bytes) |
Encapsulated PostScript
(343 kB) |
PDF
(91 kB) ]
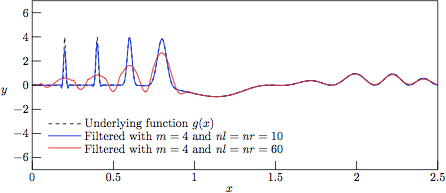
Figure 6.
The profiles resulting from Savitzky—Golay-filtering of the test
function g(x) with added Gaussian noise of variance
V = 0, that is to say a direct regression against the
underlying function g(x). This figure illustrates the
limitations of the attempts of
linear regression of a polynomial to an underlying function which
clearly cannot be approximated by a simple polynomial expressin in
certain domains. One should always keep this limitation in mind before
accepting (or discarding) data filtered by the Savitzky—Golay algorithm,
despite the many cases in which it performs exceptionally well.
[ MetaPost code
(779 bytes) |
Encapsulated PostScript
(275 kB) |
PDF
(68 kB) ]
References
[1] For information on the CWEB programming language as written by Donald E. Knuth, as well as samples of CWEB programs, see Knuth's homepage at http://www-cs-faculty.stanford.edu/~knuth/cweb.html For information on literate programming, as well as additional CWEB examples, see http://www.literateprogramming.com
[2] A. Savitzky and M. J. E. Golay, Smoothing and Differentiation of Data by Simplified Least Squares Procedures, Analytical Chemistry 36, 1627-1639 (1964). This paper is available at http://dx.doi.org/10.1021/ac60214a047.
[3] Abraham Savitzky (1919--1999) was an American analytical chemist. http://en.wikipedia.org/wiki/Abraham_Savitzky
[4] Marcel J. E. Golay (1902-1989) was a Swiss-born mathematician, physicist, and information theorist, who applied mathematics to real-world military and industrial problems. http://en.wikipedia.org/wiki/Marcel_J._E._Golay
[5] J. Riordon, E. Zubritsky, and A. Newman, Analytical Chemistry looks at 10 seminal papers, Analytical Chemistry 72, 324 A (2000). This paper is publicly available for download at http://pubs.acs.org/doi/pdf/10.1021/ac002801q.
[6] For information on the Portable Document Format (PDF) of Adobe, see for example the homepage of Adobe Systems Inc., at http://www.adobe.com/products/acrobat/
[7] For information on the PostScript programming language, see for example the PostScript area on the website of Adobe Systems Inc., at http://www.adobe.com/products/postscript/ or the reference book "PostScript Language - Tutorial and Cookbook" (Adison-Wesley, Reading, Massachusetts, 1985), ISBN 0-201-10179-3.
[8] The resulting test data, which so far has not been subject to any filtering, may easily be viewed by running the following script in Octave/Matlab:
clear all; close all;
hold on;
u=load('example-2.0.dat'); plot(u(:,1),u(:,2),'-b');
u=load('example-1.0.dat'); plot(u(:,1),u(:,2),'-c');
u=load('example-0.5.dat'); plot(u(:,1),u(:,2),'-r');
u=load('example-0.0.dat'); plot(u(:,1),u(:,2),'-k');
legend('var(f(x))=2.0','var(f(x))=1.0','var(f(x))=0.5','var(f(x))=0.0');
hold off;
title('Artificial data generated for tests of S-G filtering');
xlabel('x');
ylabel('f(x)');
[9] MetaPost is both a programming language and the only known interpreter of the MetaPost programming language. Both are derived from Donald E. Knuth's Metafont language and interpreter. The language shares Metafont's elegant declarative syntax for manipulating lines, curves, points and geometric transformations [Wikipedia]. The originator of MetaPost, John Hobby, has a page on the MetaPost language at http://cm.bell-labs.com/who/hobby/MetaPost.html. The TeX Users Group (TUG) has tutorials and links to MetaPost resources listed at http://www.tug.org/metapost.html.
[10] For information on the TeX typesetting system, as well as on the dvips program, see for example the website of the TeX Users Group, at http://www.tug.org